從剪切應變的公式中,α (γne) 斜角 (rake angle)為已知的刀具資料,所以只剩下剪切角 ψ 為未知數,在第三節中曾經以切屑 a0 與未變形切屑 ac 跟斜角計算剪切角的值:
如果在切屑資料不明確的況下,可以從能量的角度來估算剪切角的可能數值。
當知道了剪切角,後續要計算力量、應力、應變、應變率、速度跟能量都會變得比較容易。
Merchant 假設當切削作工達到一個所需要的能量最小值時,剪切應力最會使材料發生剪切變形,對應發生剪切角,也就是作功 Fc * V ,當 V 固定,所以會有一個剪切角的數值使得 切削力達到所需要的最小值,而且不會再變化,也就是若將 Fc視為剪切角的函數,此時函數的斜率 d Fc / dψ應該為零。
因此可以從剪切力跟切削力加上剪切力跟剪切應力的公式:
將 Fc 除以 Fs ,再將 Fs 以剪應力公式代入,可以得到切削力的公式如下:
假設不考慮彈性變形的完全塑性作用,跟已知或固定值的 Ac、τs、β、α,跟 d Fc / d ψ為零,可以得到ψ、α、β的關係如下:
從以下圖示兩種大小的剪切角示意圖:
在材料固定,剪切強度(應力)固定的情況下,可以看出來當剪切角越大,剪切面的面積越小,所需要的剪切力也就越小;反之剪切角越小,剪切面積越大,所需要的剪切力越大。
所以從剪切角與斜角跟磨擦角的關係式可以得到以下兩個結論:
增加斜角的值可以增加剪切角,降低所需切削力
減少磨擦角的值 (等於是降低磨擦係數) 可以增加剪切角,降低所需切削力
這跟直覺上的刀具越銳利切削力愈小,以及磨擦越小切削力越小是完全相符的。
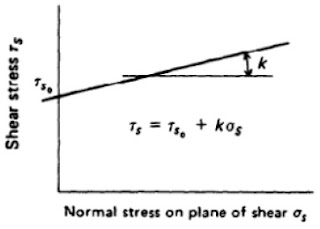
實務上如果以粉末冶金材料燒結製造的碳化物 ( carbide )刀具切削鋼材時,剪切強度(應力)會跟正向應力(強度)有關,但是正向應力強度並不是固定不變的 (例如應變硬化,strain hardening),所以如果將剪切強度以 τs= τ0+ k*σs
代入切削力公式,同樣以 d Fc / d ψ=0的關係可以得到
其中 C 稱為 Merchant constant:
實驗上的結果也符合公式的預測,比第一個公式更接近鋼材的切削結果:
後續有多個研究,針對不同材質特性或考量BUE的影響,改變或增加不同的條件,導出多個剪切角與斜角、磨擦角的關係式如下表:
以磨擦角減斜角的數值為橫軸,剪切角為縱軸,不同模型(材質)可以表示如下:
不論那個模型,基本上都有兩個重點:
增加斜角的值可以增加剪切角,降低所需切削力
減少磨擦角的值 (等於是降低磨擦係數) 可以增加剪切角,降低所需切削力
剪切應力
切削中的剪切應力與一般的拉伸、彎曲、扭轉不同,通常在切削中的剪切應力強度比較高,如下圖示:
在切削過程中,切削平面上發生的材料塑性流動(變形)行為有以下幾個特色:
1. 相對比較大的應變率跟比較高的溫度
2. 切屑還沒有產生整體斷裂前,剪切面上承受的正向應力會使應變的升高到比較大的值;原文是"Moderate normal stress on the shear plane giving rise to large values of homogeneous strain without gross fracture in the chip.",不知道有沒有誤會意思。
3. 在同一時間內會在很小的體積範圍中漸進的發生變形。
4. 剪切面非常靠近相對堅硬的刀具會限制材料的流動。


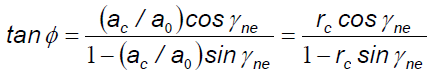











沒有留言:
張貼留言